- 一种基于模糊控制的智能控制系统的研究
-
企业: 控制网 日期: 2008-06-28 领域: 仪器仪表 点击数: 3316  郭 霞(1980-)
郭 霞(1980-)
女,内蒙古人,硕士,助教,(西安交通大学城市学院,陕西 西安 710021)研究方向为智能控制,现就职于西安交通大学城市学院。
摘要: 本文根据对二阶控制系统动态过程的的分析,利用系统偏差及偏差变化率制定和调整了模糊控制器的控制策略,并且应用到具有一定不确定性、难以建立精确数学模型的控制系统中,经过仿真试验,证明该控制策略具有无静差、响应快、精度高等优点。
关键词:模糊控制;偏差;策略Abstract: Based on the analysis for the dynamic process of the second-order control system, this paper proposes the control strategy of the fuzzy-controller by using the system deviation and deviation rate of change. Then this strategy is applied to the control systems, which are unstable and difficult to modeling. Simulation test proves that this control strategy has no stable deviation, fast-response, high-precise and so on.
Key words: Fuzzy-control;Deviation;Strategy
1 引言
模糊控制是近十几年来迅速发展的一项技术,与神经网络及专家控制并称为智能控制。由于其简单实用,目前已成功应用于各种控制系统中。模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数学控制方法,属于非线性控制方法。由于引入专家的逻辑思维方式,使得模糊控制器具有一定的自适应控制能力,因而特别适用于难于用精确数学模型描述的系统,并且有很强的鲁棒性和稳定性。
本文首先通过对二阶控制系统动态过程的的分析,将系统偏差及偏差变化率作为系统输入,制定和调整了模糊控制器的控制策略,然后把我们所研究出的控制策略应用到温度控制系统中,由于温度控制系统的对象具有大惯性、大时滞和非线性的特点,存在很多不确定的因素,所以难以建立精确的数学模型,导致控制系统性能不佳。通过试验仿真分析,可以得出本文所提出的模糊智能控制策略可实现对数学模型不确定的控制对象的满意控制,使系统具有可靠性高、使用寿命长等优点。
2 模糊控制规则的制定
众所周知,根据专家经验或过程知识可以生成模糊控制规则,当然模糊控制规则是基于手动控制策略而建立的,而手动控制策略又是人们通过学习、实验及长期经验积累而逐渐形成的,是操作者或专家的一种知识集合。手动控制过程一般是先通过对被控对象或过程的观测,操作者再根据已有的经验和技术知识,进行综合分析并作出控制决策,调整加到被控对象的控制作用,从而使系统达到预期的性能指标。
手动控制的作用同自动控制系统中的控制器的作用是基本相同的,所不同的是手动控制决策是基于操作者的经验和技术知识,而控制器的控制决策是基于某种控制算法的数值运算。
二阶系统是工程上最常见而又最重要的一类系统。通过对该类对象阶跃响应曲线的分析,结合操作者经验以及对系统动态信息的识别进行直觉推理,可以对模糊控制器的控制策略进行制定和调整。
2.1 控制系统动态过程分析
这里我们仍以二维模糊控制器为例(输入为系统偏差e及偏差变化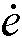 ,输出为控制量u),
,输出为控制量u),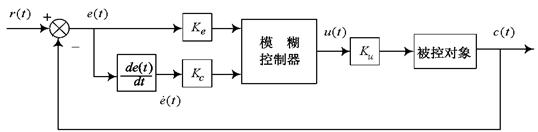
图1 二维模糊控制系统说明模糊控制器规则的制定及调整。参看图1二维模糊控制系统,被控对象为二阶振荡环节,
初步制定模糊控制器的控制规则,当r(t)为阶跃给定时,系统输出c(t)、偏差e(t)=r(t)-c(t)及偏差变化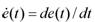 曲线如图2(a)、(b)、(c)所示。
曲线如图2(a)、(b)、(c)所示。
参看图2,系统的响应是连续的四个相位(Ⅰ、Ⅱ、Ⅲ、Ⅳ)周期重复出现,并且输出值的变化量比上个周期逐渐减小。
①相位I :图2(a)中系统输出曲线上的a1~b1段,在控制信号作用下,被控参数处于上升阶段。在这一过程中,系统响应、偏差和偏差变化的过程特性表现出,偏差e=(r-c)>0并逐渐减小;偏差变化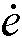 < 0并且其绝对值逐渐加大,在相位I时,e.
< 0并且其绝对值逐渐加大,在相位I时,e.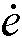 < 0,系统输出趋向给定值变化。
< 0,系统输出趋向给定值变化。
②相位Ⅱ: 图2(a)中系统输出曲线上的段。这一过程中,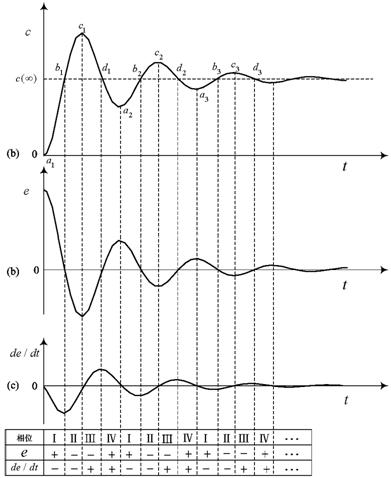
图2 二阶被控对象系统输出、偏差及偏差变化曲线系统输出值已超出了给定值,偏差e=(r-c)<0并且其绝对值逐渐加大;在这一过程中,系统响应、偏差和偏差变化的过程特性表现出,偏差e=(r-c)<0(图2(b)) ;偏差变化
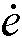 < 0(图2(c))并且其绝对值逐渐减小,在相位Ⅱ时,e.
< 0(图2(c))并且其绝对值逐渐减小,在相位Ⅱ时,e.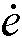 > 0,系统输出背离给定值方向变化。
> 0,系统输出背离给定值方向变化。
③相位III: 图2(a)中系统输出曲线上的c1~d1段。这一过程中,系统输出值减小,但是偏差e=(r-c)<0(图2(b),其绝对值逐渐减小;偏差变化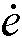 > 0(图2中(c))。在相位Ⅲ时,e.
> 0(图2中(c))。在相位Ⅲ时,e.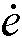 < 0,系统输出朝向给定值方向变化。
< 0,系统输出朝向给定值方向变化。
④相位IV: 图2(a)中系统输出曲线上的d1~a2段。在这一过程中,系统响应、偏差和偏差变化的过程特性表现出,偏差e=(r-c)>0(图2(b))并逐渐变大;偏差变化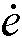 > 0(图2(c))并且逐渐减小,在相位Ⅳ时,e.
> 0(图2(c))并且逐渐减小,在相位Ⅳ时,e.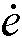 < 0,系统输出背离给定值方向变化。
< 0,系统输出背离给定值方向变化。
之后,控制系统重复Ⅰ、Ⅱ、Ⅲ、Ⅳ相位过程,但是偏差以及偏差变化的数量级逐渐变小,其模糊语言值减小。将上述系统响应曲线的不同阶段,偏差e、e&、e×e&及系统响应变化趋势c用表1表示出来。
由表1可以看出,四个相位区中,e×e&>0(表中相位Ⅱ、Ⅳ),系统响应背离给定值;当e×e&<0时,系统响应趋向给定值(表中相位Ⅰ、Ⅲ)。
表1 偏差、偏差变化、及系统输出的变化趋势
相位I
相位II
相位III
相位IV
偏差e
>0
<0
<0
>0
偏差变化e&
<0
<0
>0
>0
e×e&
<0
>0
<0
>0
c的变化趋势
趋向给定值
背离给定值
趋向给定值
背离给定值
2.2 模糊控制规则的调整
十字交叉规则库的形式如表2所示。如前所述,输入变量分别为偏差e及偏差变化e&,输出为控制量u。所谓十字交叉,就是我们首先写出输入变量e及e&的模糊语言值为“Z0”时的控制规则。如当e&的值为“Z0”时,控制量u的模糊语言值按输入变量e的值确定,即规则为:
If e is NL and e& is Z0 Then u is NL
If e is NM and e& is Z0 Then u is NM
L
If e is PL and e& is Z0 Then u is PL
如表2中间的一列。上述规则的物理意义是很明显的,输入变量偏差变化e&为Z0,即意味着偏差e处于极值状态。见图2,当偏差为e=r-c为NL时,系统超调大,当然应施加一个u为NL的控制量能够尽快地将被控参数c调节到给定值上,其它情况类推。
表2 十字交叉规则库
u
输入变量e&
NL
NM
NS
Z0
PS
PM
PL
输
入
变
量
eNL
NL
NM
NM
NS
NS
Z0
NM
NS
NS
Z0
PS
PS
PM
PS
PS
PM
PM
PL
PL
仍然参看图2,当输入变量偏差e为Z0,即意味着偏差e&处于极值状态。控制量u的模糊语言值按输入变量e&的值确定,即规则为:
If e is Z0 and e& is NL Then u is NL
If e is Z0 and e& is NM Then u is NM
L
If e is Z0 and e& is PL Then u is PL
表2中间地一行,这样就形成了一个十字交叉的控制规则。
十字交叉规则写出之后,表2中明显出现四个空白区,即
⑴偏差e>0,偏差变化e&<0,e.e&<0;
⑵偏差e<0,偏差变化e&<0,e.e&>0;
⑶偏差e<0,偏差变化e&>0,e.e&<0;
⑷偏差e>0,偏差变化e&>0,e.e&>0。
① 依据前面的分析,如表1所列的那样,写出上述四个空白区控制规则的物理意义就明确了。偏差e>0,偏差变化e&<0,e.e&<0,相当于图2中的相位Ⅰ。偏差为正,偏差变化为负,系统输出朝向给定值的方向变化。值得注意的是,由图2可知,偏差e及偏差变化e&不会同时获得极值。但是从系统动态过程分析来看,如果偏差e为“PL”,且偏差变化e&为 “NL”时,则说明尽管偏差e较大,但在迅速地减小,系统输出c朝向给定值的方向变化快,如果控制量u为“P”,则系统就会超调,因而在这种情况下,控制器输出u可以为“Z0”,其规则为:
If e is PL and e& is NL Then u is Z0
当偏差e减小,如为“PS”,而偏差变化e&为 “NL”时,说明在小的正偏差下,系统输出c朝向给定值的方向变化快,为了拟制系统可能的超调的趋势,不仅控制量u不为“P”,而且应为“N”,其规则可以是
If e is PS and e& is NL Then u is NS
② 偏差e<0,偏差变化e&<0,e.e&>0,相当于图2中的相位Ⅱ。系统超调,且继续向背离给定值方向变化,为了使系统输出尽快靠拢给定值,模糊控制器的输出u为“N”,且绝对值较大,例如当e为“NS”,e&为“NL”时,其控制规则可以是
If e is NS and e& is NL Then u is NL
该规则说明,虽然偏差e不大,但偏差变化速度较快,因而为被控对象施加一个较大的负向控制量。
③ 偏差e<0,偏差变化e&>0,e.e&<0,相当于图2中的相位Ⅲ。系统输出c向给定值方向变化。为了防止系统失调(系统输出低于给定值),在偏差|e|较大时,若偏差变化e&较大,系统输出c向给定值方向变化快,控制规则可以是
If e is NL and e& is PL Then u is Z0
If e is NS and e& is PL Then u is PS
上述两条规则说明,当偏差e为“NL”,偏差变化e&为“PL”时,可以使控制量u为零,使系统输出向着给定值方向变化;而当偏差e为“NS”,偏差变化e&为“PL”时,虽然偏差数量不大,但系统输出向着给定值方向变化快,因而模糊控制器可以提供一个较小的正控制量“PS”,用于拟制系统失调的劲头。
④ 偏差e>0,偏差变化e&>0,e.e&>0,相当于图2中的相位Ⅳ。这种情况与相位Ⅱ是一样的,只是系统输出变化方向相反,模糊控制器提供较大的控制量u。其规则可以是
If e is PS and e& is PL Then u is PL
If e is PS and e& is PS Then u is PM等。
根据以上的论述,可以初步确定出如表3所表示的规则库。当然,我们还应该在系统仿真或系统实现中进一步调整规则库,以取得满意的控制性能指标。
表3 常见二输入、一输出的模糊控制规则表
u
输入变量e&
NL
NM
NS
Z0
PS
PM
PL
输
入
变
量
eNL
NL
NL
NL
NL
NM
NS
Z0
NM
NL
NL
NM
NM
NS
Z0
Z0
NS
NL
NM
NM
NS
Z0
Z0
PS
Z0
NM
NS
NS
Z0
PS
PS
PM
PS
NS
Z0
Z0 PS
PM
PM
PL
PM
Z0
Z0
PS
PM
PM
PL
PL
PL
Z0 PS
PM
PL
PL
PL
PL
3 模糊控制系统的应用
控制工程的基本目标就是提取和应用有关怎样控制过程的知识,使得控制系统能够可靠、安全实现高性能的运行。怎样最好地控制一个过程的经验,是宝贵的知识。下面我们就论述和设计一个模糊控制系统;同时论述在设计过程中出现的新问题及其解决方案。
3.1 温度控制系统
设计一个温度模糊控制系统。被控对象为一热处理工艺过程中的加热炉,加热设备为三相交流调压供电装置,输入控制信号电压为0~5V,输出相电压0~220V,输出最大功率180KW,参看图3电加热装置示意图。
3.1.1控制系统性能指标:
① 温度调节范围:100℃~500℃;
② 系统无静差(即稳态误差为零)。
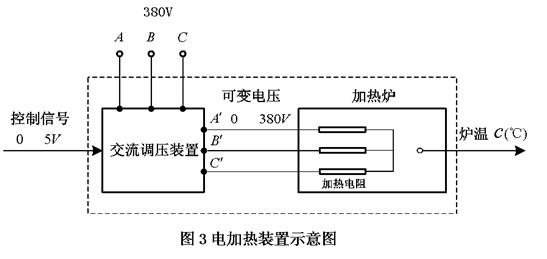
3.1.2确定控制方案
该系统被控对象为加热炉,通过改变加热电阻上的电压调节炉膛温度。图3中,从控制信号u(t)到炉膛温度c(t)可以看作广义被控对象,当控制信号u(t)=5V时,炉膛温度最高可以达到625℃,如图4所示。被控对象具有惯性特征,当然可以采用传统PID控制设计。但是,我们这里不写出被控对象的精确数学模型,设计模糊控制系统,通过与PID控制的对比,说明模糊控制的优点。
图4 广义被控对象由于设计要求为无静差控制系统,被控对象具有惯性特征,为达到设计要求,因此采用二维模糊PID控制器,参看图5。系
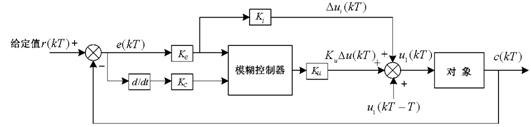
图5 模糊PID控制系统统结构采用二维模糊控制器与积分算法相结合的形式实现模糊PID控制器。首先我们对该控制方案进行分析,明确其控制特点。由图5可知,提供给被控对象的控制量为:
u1(kT)=u1(kt-T)+KuDu(kT)+KeKie(kT) (1)
式中的T为采样周期;Ku为模糊控制器输出增益系数;Ki为积分系数。
由式(1)可知,u1(kT)控制变量由三部分组成,第一部分是上一采样时刻的控制量u1(kt-T);第二部分是由模糊控制器提供的增量输出KuDu(kT);第三部分是KeKie(kT)。
对式(1)两边取Z变换,
U1(z)=z-1U1(z)+KuDU(z)+KeKiE(z)
(2)
在Z域中,1/(1-z-1)具有累加和的性质,相当于连续域中的积分。由式(3.2)可知控制变量u1(kT)是对以下两项积分的结果:第一项是模糊控制器提供的增量输出KuDu(kT),第二项是KeKie(kT)。我们知道,如果只有第一项,根据模糊控制器的性质,当Ku(kT)=0时,其系统偏差e(kT)不一定为零,此时控制变量u1(kT)保持不变,其结果不能消除系统静态偏差。第二项是u1(kT)对KeKie(kT)的积分,理论上只有e(kT)=0,u1(kT)才能停止变化,系统达到无静差控制。
3.1.3输入、输出变量隶属函数及论域的选择
⑴ 隶属函数的选择
系统中模糊控制器采用所谓“标准”形式,即二输入、一输出变量模糊集论域均为[-6,6],采用常用的三角形隶属函数,如图6所示。
⑵ 偏差e(t)的论域及增益系统Ke值的选择
对于模糊控制器来说,输入变量的论域,根据专家的经验,如果认为系统偏差e(t)=r(t)-c(t)的值大于、等于30℃就应该是语言值的最大值“PL”, e(t)的值小于、等于-30℃就是“NL”,因此偏差e(t)的论域为[-30 30],Ke的初选值为:
30.Ke=6
则 Ke=6/30=0.2
如果根据专家的经验,系统偏差e(t)=r(t)-c(t)的值大于、等于20℃就应该是语言值的最大值“PL”, e(t)的值小于、等于-20℃就是“NL”,那么偏差e(t)的论域为[-20 20],Ke的初选值为
20.Ke=6
则 Ke=6/20=0.3
设计中,我们初步选定Ke=0.3。
值得说明的是,模糊控制器输入变量偏差e(t)的论域并不等于系统运行过程中偏差的范围,例如我们要设计的加热炉控制系统,在给定值为400℃时,若加热炉的初始温度为室温25℃,则系统的初始偏差为e(0)=400-25=375℃。但是,从控制的角度来说,偏差e(t)≥30℃时,专家就可能认为是模糊最大值“PL”。
⑶ 偏差变化(t)=de(t)/dt的论域及增益系统Kc的选择
类似于偏差e(t),如果能够知道e&(t)的变化范围,就可以在该范围内确定e&(t)输入到模糊控制器的论域。应该注意到的是,该论域小于e&(t)的变化范围。初步选择出Kc的值后,经仿真或实验修正Kc的值,以便达到满意的系统性能指标。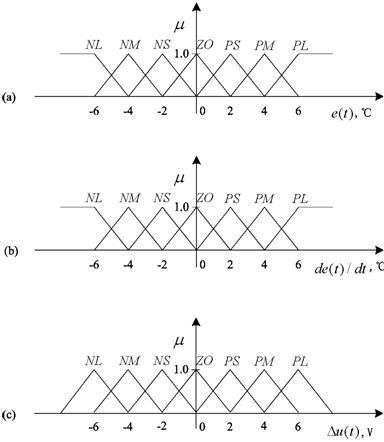
图6 模糊控制器的隶属函数根据被控对象在系统运行中偏差变化e&(t)的范围,选择e&(t)的论域及系数Kc。因为
e(t)=r(t)-c(t) (3)
de(t)/dt=dr(t)/dt-dc(t)/dt (4)
当r(t)为常数时,de(t)/dt=0,因此
de(t)/dt=-dc(t)/dt (5)
由式(3.5)可知,在恒定给定的情况下,偏差变化速率(t)=de(t)/dt等于被控对象输出变化速率,只是相差一个负号,即-dc(t)/dt。被控对象在阶跃输入下其输出响应变化的速率最大。因此,需要对被控对象做一个简单的阶跃响应试验。
一般来说,若被控对象本身为稳定的情况下(即最小相位环节),其阶跃响应为过阻尼和欠阻尼两种情况,现在分别来讨论这两种情况下的响应速率问题。
① 阶跃响应为过阻尼的情况
参看图4所示,其控制输入量u(t)=(0~5)V,对象输出为c(t)=(0~5)℃,这些数据在设计的开始阶段是很容易获得的。现在给广义对象施加一个控制电压u(t)=4V的阶跃输入,广义对象的响应如图6所示。
观察图6,对象响应曲线稳定在500℃,计算由0℃上升到稳态值500℃的63.2%,即
500×63.2%=316(℃)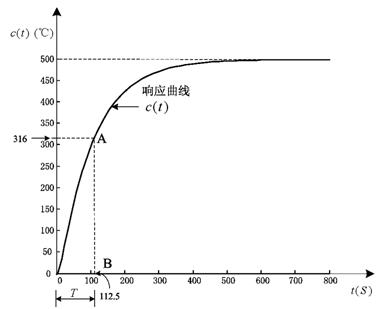
图7 被控对象过阻尼阶跃响应在图6的纵坐标上316℃处作水平线与响应曲线c(t)相交于A点,由A点作垂线与横坐标相交于B点,横坐标上由0到B点的距离我们称为对象的估计时间常数T(将对象等效为具有一阶惯性特征),由图6知,T=112.5S。在这种情况下,对象的最大响应速率为:
e&(t)=316 / 112.5=2.81(℃/S)
因而,对于恒定给定来说,偏差变化率|e&(t)|的最大值为2.81℃/S。类似于偏差e(t),考虑到实际运行控制情况时,偏差变化e&(t)输入到模糊控制器的模糊集论域应在|e&(t)|的最大值为2.81℃/S以内选择。例如,选择模糊集论域为|e&(t)|的最大值的五分之一,即
2.81×0.2=0.562(℃/S)
则e&(t)的模糊集论域为[-0.562,0.562]℃/S。那么,Kc的初选值为:
Kc=6 / 0.562=10.67
② 阶跃响应为欠阻尼的情况
如果被控对象的阶跃响应是欠阻尼的情况,响应曲线c(t)超调并振荡衰减趋于稳态值,见图7。对象响应的最大变化率估计算法是:c(t)上升与稳态值500℃相交于A点,由A点作垂线与横坐标相交于B点,横坐标上由0到B点称为c(t)的上升时间tr,图7中tr=75S,e&(t)的估计值为:
500 / 75=6.67(℃/S)
因而,对于恒定给定来说,偏差变化率|e&(t)|的最大值为6.67℃/S。和过阻尼的情况一样,如果选择e&(t)时模糊集论域为|e&(t)|的最大值为6.67℃/S的五分之一,即
6.67×0.2=1.334(℃/S)
则e&(t)的模糊集论域为[-1.334, 1.334]℃/S。增益系数Kc的初选值为:
Kc=6 / 1.334=4.5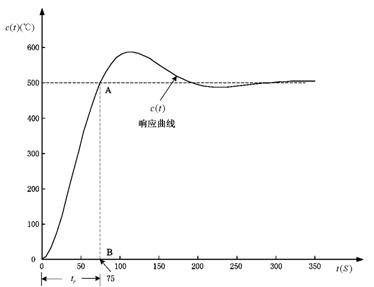
图8 被控对象阶跃响应为欠阻尼的情况⑷ 模糊控制器输出u(kT)论域及增益系数Ku的选择
如图4所示,模糊控制器采用增量输出方式,输出量为u(kT),论域为[-6,6], Ku.u(t)表示在一个采样用周期内,控制变量u1(t)的增量,显然最大增量值为6Ku。由图5可知,控制量u1(t)的论域为[0,5]V,其最大值为5V,最大增量u1(t)一般是u1(t)最大值的%位,如选u1(t)为5×2%=0.1,那么Ku的初选值为
Ku=0.1/6=0.0167
⑸ 增量积分系数Ki的选择
由控制理论可知,积分的作用就在于消除系统静态偏差,系统偏差较大时,系统由PD模糊控制器起调节作用,当系统偏差较小时,积分作用能够消除系统偏差。由图4.27看出,增量积分控制环节的输入论域为[-6,6],当偏差|e&(t)|=6时,初步设定积分增量为
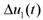 =6×1%=0.06
=6×1%=0.06
Ki选的大,调节过快,上升时间短,系统超调可能较大;Ki选的过小,过渡时间较长。因此,初步选择
Ki=0.01
3.1.4 控制规则表
根据专家的控制知识,制定控制规则表,如表3所示。值得注意的是,模糊控制器中,规则的制定要满足一定的要求:
⑴ 从直觉上看,模糊控制算法应该总能为每个过程状态推理得到一个合适的控制作用,这个特性称作“完备性”。就是说不能有失控的情况出现。
⑵ 模糊控制规则数
由于在选择最佳模糊控制规则数时需要考虑一系列的因素(如控制器的性能、计算效率、操作工的行为和语言变量的选择等),所以不存在一种通用的确定方法。在一般小系统中也许只用几条规则,但在大型系统中就可能要用几百条规则。虽然模糊控制规则数的确定具有一定的随意性,并且可以在设计、调试过程中,甚至在已经完成之后都可随时增加新的规则,但是模糊控制规则数的增加会导致系统响应速度变慢,有可能会影响控制的实时性。
⑶ 模糊控制规则的一致性
模糊控制规则的生成是基于人工操作的经验,那么规则要服从不同的性能标准。实践中,对规则的一致性进行检查,尽量减少出现互相矛盾的规则,见表3。
3.1.5根据前面论述的方法,可以离线计算出模糊控制器控制表(见表4)
表4 在线推理模糊控制器控制规则表
控制量u
输入变量偏差变化e&
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
输
入
变
量
偏
差
e-6
-6
-6
-6
-6
-6
-6
-6
-5
-4
-3
-2
-1
0
-5
-6
-6
-6
-5.5
-5
-5
-5
-4
-3
-2
-1
0
1
-4
-6
-6
-6
-5
-4
-4
-4
-3
-2
-1
0
1
2
-3
-6
-5.5
-5
-4.5
-4
-3.5
-3
-2
-1
-0.5
0
1
2
-2
-6
-5
-4
-4
-4
-3
-2
-1
0
0
0
1
2
-1
-5
-4
-3
-3
-3
-2
-1
0
1
1
1
2
3
0
-4
-3
-2
-2
-2
-1
0
1
2
2
2
3
4
1
-3
-2
-1
-1
-1
0
1
2
3
3
3
4
5
2
-2
-1
0
0
0
1
2
3
4
4
4
5
6
3
-1
-0.5
0
0.5
1
2
3
3.5
4
4.5
5
5.5
6
4
0
0
0
1
2
3
4
4
4
5
6
6
6
5
0
0.5
1
2
3
4
5
5
5
5.5
6
6
6
6
0
1
2
3
4
5
6
6
6
6
6
6
6
3.2 控制系统性能分析
完成了以上的初步设计,接着就可以对系统进行仿真或实验分析。有关系统仿真问题,在这里采用MATLAB中的Simulink对系统进行仿真。
要进行系统仿真,就需要被控对象的数学模型,即仿真模型。仿真模型不要求完全精确,从我们所做的简单阶跃响应实验结果中,可以写出被控对象的简单模型,依据该模型进行仿真实验,如果仿真结果证明其系统性能指标较好,改变仿真模型再进一步仿真,反复实验就能取得较满意的结果,说明所设计的模糊控制系统鲁棒性好,达到了仿真的目的,增强设计者对本设计的信心。
3.2.1仿真模型的建立
根据上面有关被控对象阶跃响应实验结果:过阻尼响应和欠阻尼响应。
(1)过阻尼响应,参看图6。这时可以将被控对象看作一阶惯性环节:
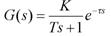 (6)
(6)
T为时间常数,T=112S;K为放大系数,阶跃响应实验时,广义对象输入控制信号为4V,对象输出稳定在500℃,因此放大系数K=500 / 4=125(℃/V)。图6中,响应输出无滞后,则 。由此,仿真模型可粗略地写为:
。由此,仿真模型可粗略地写为:
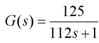 (7)
(7)
(2)欠阻尼响应
在控制工程实践中,二阶系统极为常见,并且许多高阶系统的运动特性在一定条件下可以用二阶系统的运动特性来表征。因而,对于欠阻尼阶跃响应,可以先将广义被控对象看作二阶模型。我们知道,二阶系统传递函数为:
 (8)
(8)
其中T为二阶系统的时间常数,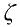 为阻尼比,
为阻尼比,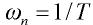 为无阻尼自然振荡频率。单位阶跃响应:
为无阻尼自然振荡频率。单位阶跃响应:
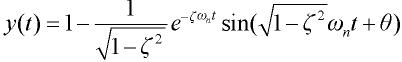 (9)
(9)
式中,
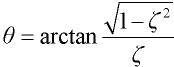 (10)
(10)
欠阻尼二阶系统的阶跃响应与特征参数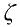 和T(或Wn)有关:
和T(或Wn)有关:
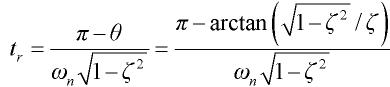 (11)
(11)
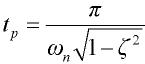 (12)
(12)
参看图9阶跃响应曲线,测量出上升时间tr=75S及峰值时间tp=115S。
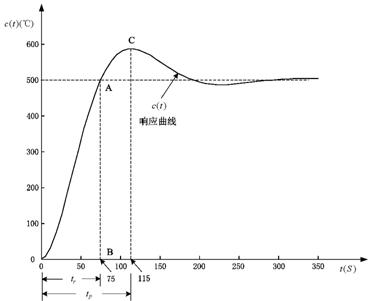
图9 欠阻尼阶跃响应情况由式(11)和式(12)计算出二阶模型的参数:
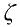 =0.46,
=0.46, 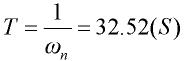
因而,被控对象的二阶参考模型为:
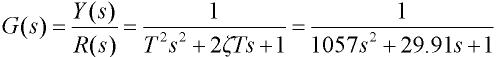 (13)
(13)
被控对象阶跃输入为4V时,对象输出稳定在500℃,因而到广义对象的放大系数
K=500/4=125(℃/V)
系统仿真模型
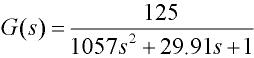 (14)
(14)
3.2.2 仿真系统框图
有了对象的初步模型,就可以对模糊控制系统进行仿真,用MATLAB中的Simulink画出系统仿真图,如图10所示。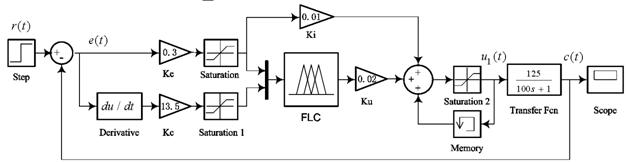
图10 系统仿真框图图中的模糊控制器FLC可以是离线计算好的控制表,也可以采样Fuzzy Tool在线推理。模糊控制器的两个输入上限幅均为6下限幅为-6;控制信号u1(t)的上限幅为5V,下限幅为0V。
⑴ 首先按照上面初选的一组参数Ke=0.3,Kc=13.5,Ku=0.02,Ke=0.01进行仿真,当系统输入为阶跃信号r(t)=400℃时,其系统响应如图10所示。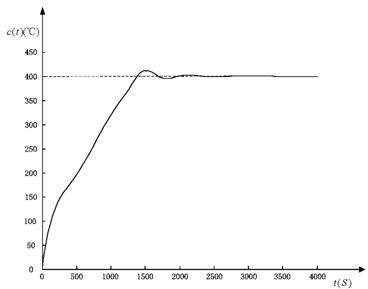
图11 阶跃给定系统响应系统无静差,系统最大超调15℃。
⑵ 将系数Ke变小,其它参数不变,如Ke=0.1,Kc=13.5,Ku=0.02,Ke=0.01再次仿真,其系统响应如图11所示。系统超调明显减小,最大超调量为2℃。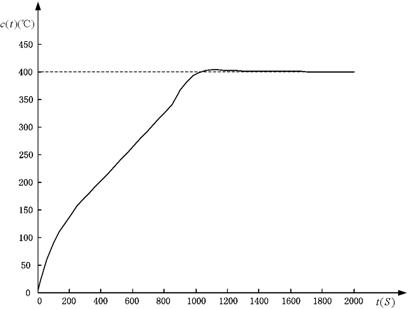
图12 系数Ke变小时,系统阶跃响应⑶ 在系统参数保持不变的情况下,Ke=0.1,Kc=13.5,Ku=0.02,Ke=0.01,改变被控对象的模型,再次仿真。参看图12系统阶跃响应曲线。
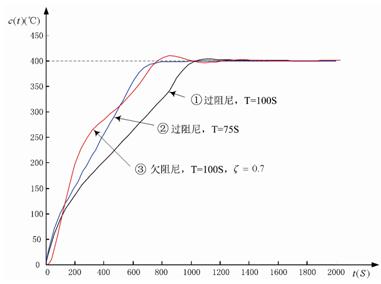
图13 改变被控对象数学模型时系统阶跃响应曲线①对应被控对象数学模型为
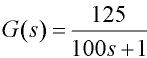 ;曲线②对应被控对象数学模型为
;曲线②对应被控对象数学模型为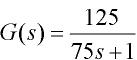 ;曲线③对应被控对象数学模型为
;曲线③对应被控对象数学模型为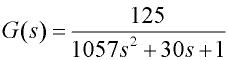 。
。
4 结束语
通过理论分析和仿真实验均表明本文所提出的控制策略是可行的,尤其是对于一些具有不确定性、难以建立精确数学模型的控制系统,不但可以使系统达到无静差,提高它的响应速度,还具有非常广泛的适用性,具有推广应用的价值。参考文献:
[1]李人厚.智能控制理论和方法 .西安:西安交通大学出版社,1994.
[2]易继锴,侯媛彬.智能控制技术 .北京:北京工业大学出版社,1999.
[3]席爱民.计算机控制系统,西安:陕西科学技术出版社,1994.
[4]黄忠霖.控制系统MATLAB计算及仿真.北京:国防工业出版社,2001
[5]沈辉.精通SIMULINK系统仿真与控制 .北京:北京大学出版社,2003.
编号:080534
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



