- 人工免疫聚类算法在交通时段自动划分上的应用
-
企业: 控制网 日期: 2008-03-02 领域: 仪器仪表 点击数: 2416  刘强(1979-)
刘强(1979-)
男,辽宁工业大学研究生,(辽宁工业大学信息科学与工程学院,辽宁 锦州 121001 ),研究方向为智能控制。
摘要:论文基于免疫网络理论和克隆选择原理,建立了一种人工免疫数据聚类分析算法,并详细阐述了聚类算法在城市交通时段自动划分中的具体应用。实例分析表明,该算法可以有效减少聚类数据的冗余信息,特别适合于解决分级聚类等传统方法不适应的大数据量聚类问题,对解决城市交通时段的自动划分等数据聚类问题是可行的和有效的。
关键词:聚类;人工免疫系统;模式识别;交通控制Abstract: An artificial immune algorithm for data clustering is proposed in this paper. This work is mainly based on the immune network theory and the clone selection principle extracted from vertebrate immune systems. Experiments show that the given clustering algorithm can effectively reduce the redundant information of data, and thus, especially fit to the mass data clustering applications where hierarchical clustering algorithm or other traditional clustering algorithms may be ineffective.
Key words: clustering;artificial immune system;pattern recognition;traffic signal control
1 引言
目前城市交通信号控制应用较为普遍的是多时段定时控制方案。多时段定时控制(time of day,TOD)是根据车流量等交通信息把一天划分为若干个时间段,不同的时段采用不同的信号优化控制方案。TOD控制的前提是交通时段的合理划分。传统上,交通工程技术人员根据收集到的交通流量,绘制流量时间曲线图,根据曲线的特征人工划分交通时段。传统方法具有很大的主观性,极易产生不合理的时段划分,难以满足现代城市交通模式快速变化的需求。
以生物免疫系统为基础的人工免疫系统(artificial immune systems, AIS) [1]已成为目前国内外计算智能领域一个新的研究热点。本文在详细研究生物免疫学和AIS的最新研究成果的基础上,建立了一种人工免疫数据聚类分析算法,该算法可以有效减少聚类数据的冗余信息,特别适合于解决分级聚类等传统聚类方法不适应的大数据量聚类问题。论文把建立的人工免疫算法用于城市交通时段的自动划分[2],克服了人工时段划分的不合理性,为TOD交通时段的划分及城市交通控制方案的制定提供了一条新的思路[3]。
2 免疫系统的基本理论
生物免疫系统是一个由细胞、分子和器官组成的复杂系统,其主要功能是限制异物对肌体的侵害[4]。免疫系统抵御外部入侵,使其机体免受病原侵害的应答反应称为免疫(immunity)。外部有害病原入侵机体并激活免疫细胞,诱导其发生反应的过程称为免疫应答。诱导免疫系统产生免疫应答的物质称为抗原(antigen,简称Ag),能与抗原进行特异性结合的免疫细胞称为抗体(antibody, 简称Ab)。抗原与抗体的结合强度用亲和度(affinity)度量。AIS主要涉及T细胞和B细胞的相关免疫特性。B细胞的作用是识别抗原和分泌抗体,T细胞能够促进和抑制B细胞的产生与分化。免疫系统的结构示意如图1所示。生物免疫学的研究成果是AIS的理论基础。本文给出的数据聚类算法,主要基于生物免疫隐喻的克隆选择理论[5]和免疫网络理论[6]。当淋巴细胞实现对抗原的识别,即抗体与抗原的亲和度(affinity)超过一定阈值后,B细胞被激活并增殖复制产生细胞克隆。由于遗传和免疫细胞在增殖中的基因突变,形成了免疫细胞的多样性。当每一种抗原侵入机体后都能在机体内选择出能识别和消灭相应抗原的免疫细胞克隆,使之激活、分化和增殖,进行免疫应答以最终清除抗原。克隆选择的主要特征是免疫细胞在抗原刺激下产生克隆扩增,随后通过遗传变异分化为多样性效应细胞和记忆细胞。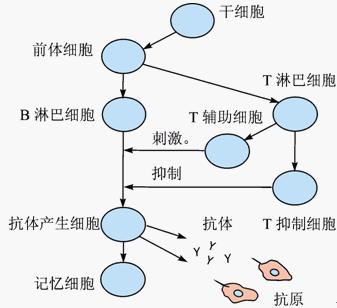
图1 免疫系统的基本结构3 人工免疫聚类分析算法
AIS借鉴了一些生物免疫系统的功能、原理和模型,使用学习、记忆和关联检索来完成识别与分类任务,具有强大的和鲁棒的信息处理能力,是一种有效的数据聚类分析方法[7]。AIS将待分析的数据作为抗原,通过抗体对抗原的学习、记忆过程来识别、分类不同数据,并从中找出数据间的相关性能。
假设标称为[0,1]下的Q个输入数据集构成抗原Ag,聚类分析的目的就是要通过免疫学习,寻找记忆数据集M作为输入数据的聚类。
为描述算法的方便,定义如下变量:
Ag:输入抗原,即待聚类的输入数据集合,或研究问题的论域:
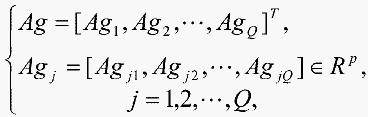 (1)
(1)
Ab:抗体,即N个初始网络细胞:
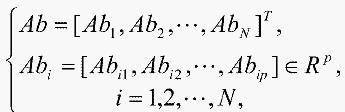 (2)
(2)
M:记忆数据集,即nt个网络记忆细胞:
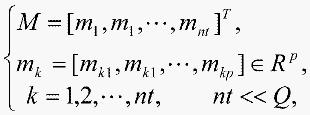 (3)
(3)
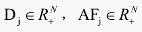 :所有抗体与抗原Agj的距离度量矢量和亲和力矢量;
:所有抗体与抗原Agj的距离度量矢量和亲和力矢量;
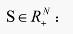 :M中抗体的相似度矢量;
:M中抗体的相似度矢量;
Nc:激发细胞产生的克隆细胞数量;
Cj:激发细胞产生的克隆细胞群体,亲和力成熟后变为C。
基于免疫网络理论和克隆选择原理的人工免疫聚类算法由如下步骤构成[5,6,7,8]:
Step1 随机初始化N个抗体Ab,作为初始网络细胞。
Step2 设定循环控制参数。
Step3 输入待聚类数据作为抗原,对抗原Agj(j=1,2,…,Q)进行如下操作:
Step3.1 计算距离度量矢量Dj和亲和力矢量AFj:
抗原与抗体之间的距离用欧几里德距离定义,即
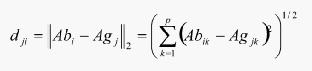 (4)
(4)
根据聚类分析的特点,抗原与抗体之间的亲和力采用式(5)定义:
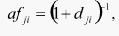 (5)
(5)
于是
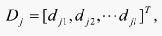 (6)
(6)
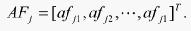 (7)
(7)
Step3.2按照opR(optimal selecting Rate)的比率从Ab中选择n个与Agj具有最高亲和力的抗体进行克隆扩增,产生对应的克隆细胞集合Cj。根据克隆选择原理,抗体与抗原的亲和力越大,抗体产生的克隆细胞数量越多。对n个选择细胞按亲和力从小到大的顺序排序,克隆细胞的数量按下式计算。
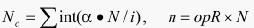 (8)
(8)
式中:Nc为n个抗体产生的克隆细胞总数;α为乘数因子,用于控制克隆群体的规模;Int(.)为取整函数。
Step3.3 应用式(9)对克隆的抗体进行随机变异操作,实现亲和力的成熟,产生具有更高亲和力的抗体细胞C。
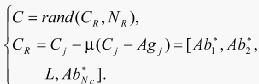 (9)
(9)
式中:rand(CR,NR)为随机函数,表示从CR中随机抽取NR个变量;μ为抗体的变异率。生物免疫系统抗体变异的实质是基因片断的重组,使得子代抗体与抗原的亲和力得以迅速提高,而且与抗原具有较大亲和力的抗体具有较小的变异率。抗体的变异率按式(10)确定:
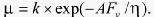 (10)
(10)
式中:AFv为抗体亲和力的标称值,k为比例因子,η为衰减控制系数。k与η的合理取值可以保证变异个体在其允许的域值范围[0,1]之内。
Step3.4 计算C的抗体细胞与抗原Agj的亲和力矢量AFc j。
Step3.5 按照rsR(re-selecting Rate)的比率,选择C中若干个与抗原Agj具有最高亲和力的抗体,作为部分记忆细胞Mp 。
Step3.6 去除Mp中相似度sij小于阈值σd的抗体,产生新的记忆集Mk ,实现免疫系统克隆抑制的效果。抗体的相似度sij用抗体间的欧几里德距离描述,即:
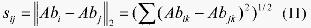 (11)
(11)
Step3.7 把部分记忆细胞Mk合并到记忆细胞集合M(M [M;Mk])。
Step4 计算M中各记忆细胞的相似度矢量S,去除M中相似度sij低于阈值σs的抗体,实现不同克隆集的网络抑制。sij按式(11)计算。
Step5 按照wsR(worst selecting Rate)的比率,随机产生若干个抗体替换原抗体中亲和力较低的个体,体现免疫系统的自组织功能。
Step6 变量替换,返回Step3,进行下一代的网络学习,直到达到要求的学习代数,或满足设定的聚类迭代要求(如迭代达到了预定的记忆细胞的个数或抗原与记忆细胞的平均亲和力达到了预定的误差范围等)。
学习过程结束后,算法的输出M为聚类数据的记忆数据集,S为记忆数据集各抗体之间的相似度。根据待聚类数据与各记忆细胞的距离,或抗原与记忆细胞的亲和度,可方便的实现对抗原数据的聚类。上述聚类算法的核心是保持网络抗体代克隆、变异及抑制的操作,最终产生记忆数据集。
调节抑制阈值σs可以控制网络的学习规模和性能,阈值越大,得到的免疫记忆数据越多,分类密度越大,数据的相似性越高。算法中其他参数的选择原则如下:初始化抗体个数N根据经验选定,其大小不影响聚类结果,但选择过大影响计算速度,过小则体现不了抗原特征,一般取N=20。克隆乘数因子α的选择取决于初始抗体的个数N。最佳抗体选择率opR一般取初始抗体的10%到20%,但opR的取值应保证每代至少有一个最优抗体克隆扩增。最差抗体选择率wsR体现免疫系统的自组织特性,一般取值不应超过10%。从抗体多样性的角度考虑,再次选择率rsR可以取较大的值,但聚类的目的是减少数据冗余信息,rsR不易太大,一般取克隆细胞的10%作为部分记忆细胞。
4 交通时段的免疫聚类研究
交通时段的人工免疫聚类分析分两步进行:第一步将交通数据看作免疫系统的抗原;第二步采用常规的聚类分析方法,对交通流量的免疫记忆集做聚类分析,实现交通时段的自动划分。
交通工程实践中,一般以15min的交通流量为基础进行交通时段的划分,将一天的96个交通流量数据作为免疫系统的抗原。
4.1 交通数据的预处理
考虑交通数据变化较大(如白天峰值时段的交通流量与夜晚谷值时段的交通流量相差十分悬殊),聚类前首先应用式(12)对交通数据做标准化变换处理:
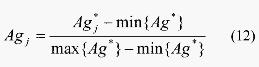 (12)
(12)
式中“*”表示交通流量的原始数据。聚类实践表明,如果直接应用每天的交通数据进行聚类,结果存在文献[2]指出的“时段冲突”或“聚类重叠”,即同一时间段在不同的工作日(如每周的星期一)归属于不同的类。(3节中各式的p=1,Ag,Ab,M等矩阵均降为同维列向量)。
4.2 交通时段聚类分析实例
本文结合现实应用的需要,利用锦州交警支队提供的解放路的交通数据库,进行基于人工免疫算法的交通聚类研究,实现城市交通时段的自动划分。图2为根据历史交通数据的96个平均流量绘制的解放路与士英街路口星期一的交通流量时间曲线图。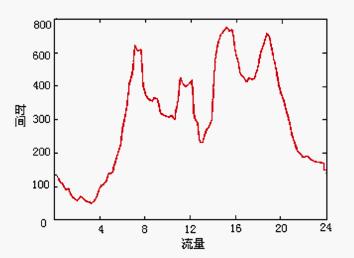
图2 24小时平均交通流量曲线把上述96个平均交通流量作为抗原应用于3节的人工免疫聚类算法,进行免疫识别和记忆。算法中的参数设置如下:初始化抗体个数N=20;最佳抗体选择率opR=20%;克隆乘数因子α =1;再次选择率rsR=20%,wsR=10%;最大迭代次数NA=15;为保证抗体的多样性,σd取0.001,σs为0.05。表1是交通流数据的人工免疫计算过程,共分15代。
表1 聚类数据的人工免疫计算过程: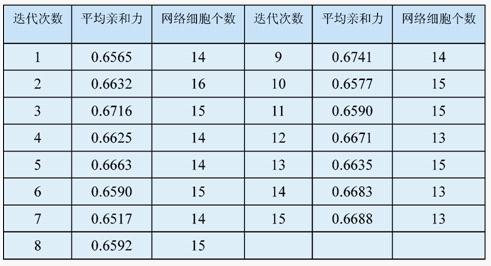
从数据分类结果可以看出第9次迭代结果,记忆数据集同抗原数据之间具有较大的平均亲和力,免疫记忆数据集的规模适中,是一种较为理想的数据分类结构。
为直观起见,将由人工免疫算法得到的记忆数据应用谱系图的方法描述如图3所示,显然,当距离值取0.1时,第9次迭代结果的14个记忆数据被清晰地分成了5类。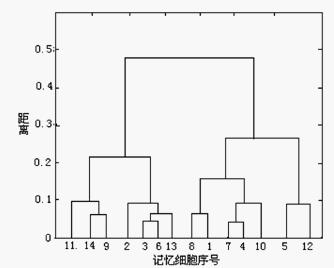
图3 交通流记忆细胞集的聚类谱系图采用重心法计算各交通数据与记忆类重心之间的距离,进行交通数据的二次聚类,并与其交通时段对应,得到解放路与士英街路口星期一的交通时段划分情况如图4所示。即根据交通流量可以把全天分为如下几个交通时段:类I时段22:45-5:15;类II时段12:15-14:00,20:30-22:45;类III时段5:15-6:30, 8:15-11:00;类Ⅳ时段11:00-12:15,16:00- 18:00,19:15-20:30;类V时段6:30-8:15,14:00-16:00,18:00-19:15。
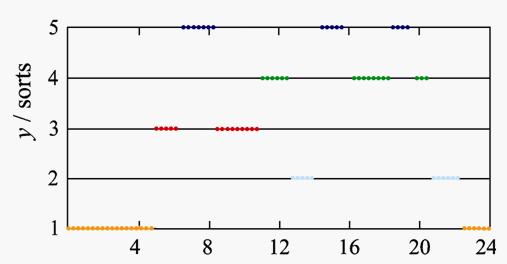
图4 TOD交通时段划分5 结束语
人工免疫数据聚类算法可以有效减少聚类数据的冗余信息,特别适合于解决分级聚类等传统方法不适应的大数据量聚类问题。作者把建立的人工免疫聚类算法应用于城市交通时段的自动划分,克服了人工时段划分的不合理性。合理设置参数的取值范围可以满足不同聚类问题的需要。其它作者:
王艳秋(1955-),女,教授,辽宁工业大学信息科学与工程学院院长,博士,硕士研究生导师,研究方向:近代交流调速系统;智能控制。
张健(1981- ),男,辽宁工业大学研究生,研究方向:智能控制。参考文献
[1]肖人彬, 王磊.人工免疫系统:原理、模型、分析及展望[J]. 计算机学报, 2002, 25 (12) : 1282 - 1291.
[2]HAUSER T, SCHERER W. Data mining tools for real time traffic signal decision support and maintenance[C]//Proc of IEEE Int Conf on Systems, Man, and Cybernetics. Tucson, USA: IEEE Press, 2001:1471-1477.
[3]PARK.B, LEE Do-Hoon, YUN Hsoo. Enhancement of Time of Day Based Traffic Signal Control [C]// Proc of IEEE Int Conf on Systems, Man, and Cybernetics. USA: IEEE Press, 2003:3619 - 3624.
[4]林学颜, 张玲. 现代细胞与分子免疫学[M].北京:科学出版社, 1999:46-62.
[5]CASTROL, ZUBENF. An evolutionary immune network for data clustering[C]// Proc of the Sixth Brazilian Symposium on Neural Networks. Janeiro: IEEE Press, 2000: 84-89.
[6]DASGU PTAD, FORRESTS. Artificial immune systems in industrial applications[C]//Proc of Second In t Conf on Intelligent Processing and Manufacturing of Materials. Honolulu, USA: IEEE Press, 1999: 257-267.
[7]Dasnupta D. Artificial Immune Systems and Their Applications[M].New York: Sprinner~Verlan, 1999.
[8]TIMM IS J, N EAL M. Artificial immune systems for data analysis [J]. B io System s, 2000, 55 (2): 143 - 150.
[9]D. K. Merchant, G. L. Nemhauser. Optimality conditions for a dynamic traffic assignment model [J]. Transportation Science B, 1978, 12: 200-207.
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



