- 降损节能的边际成本研究——无功就地补偿技术与经济结合的可行性探讨
-
企业: 控制网 日期: 2007-11-07 领域: 变频器 点击数: 1411
关键词:无功补偿;边际成本;最佳功率因数值 赖伟源 (1972-)
赖伟源 (1972-)
(广州电力局,广东 广州 510730)广东顺德人,助理工程师,大学本科,毕业于广东工业大学电气工程系电力系统及其自动化专业,研 究 方 向为如何提高直流供电电源的可靠性。
对用电设备实现无功就地补偿,就是在电力系统的终端进行无功补偿,从而实现全系统的补偿。无功就地补偿能减少无功电流的流动,即减少线路损耗,减少变压器铜损,减少电压损失,减少导线截面及提高设备利用率,降低设备增容的投资。近年来,补偿电容器不断发展,无功就地补偿装置又具有使用简单、方便、运行可靠等特点,这种节能技术已得到广泛的应用。
无功就地补偿之节能实质就是降低损耗,节约开支,提高经济效益,其技术指标主是功率因数。当功率因数为1时,补偿效果最好,但技术指标最高,并不等于效益最好。那么,使无功就地补偿技术指标高,而经济效益最好的边际成本在哪里呢?本文即对此作一分析。
1 无功就地补偿的功率因数

图1 无功就地补偿向量图
视在功率 S1=(P2+Q21)1/2 (KVA)
S2=(P2+Q22 )1/2(KVA)
补偿前无功功率为Q1(Kvar),补偿后为Q2(Kvar),在有功功率P(KW)不变的情况下,并联补偿电容器后,功率因率从CosΦ1、提高到CosΦ2,即补偿电容器容量等于用电设备减少从电源吸收的无功功率为:
Qc=P[(1/Cos2Φ1 -1)1/2 - (1/Cos2Φ2-1)1/2 ] (1)
则补偿后功率因数用补偿电容器表示为:
CosΦ2=1/[1+(tgΦ1-Qc/P)2 ]1/2 (2)
由数学知识可知,(2)式是一个单值连续函数,极值为1,如以Qc/P为横轴,CosΦ2为纵轴,得以下曲线,
如图2所示: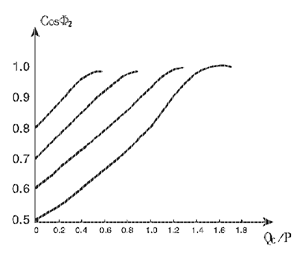
图2(从右向左,曲线依次是1,2,3,4)
1-CosΦ1=0.5 2-CosΦ1=0.6
3-CosΦ1=0.7 4-CosΦ1=0.8以CosΦ1=0.6为例,如果补偿至CosΦ2=0.95,则功率因数相对提高:
△CosΦ2=(CosΦ2-CosΦ1)/ CosΦ1=(0.95-0.6)/0.6=58%
需要补偿电容量的容量:
Qc=P
如再要CosΦ2从0.95补偿到1,则功率因数相对提高:
CosΦ2=(1-0.95)/0.95=5.3%
而需增加的电容器容量为:
Qc=0.33 P
由以上可知,前者的收益是后者的58/5.3=10.94倍,但需要的容量仅为后者的1/0.33=3.03倍,理论和实践都证明,CosΦ2越接近1,所补偿的电容量需越大,相对投资亦越大,而经济效益小。因此,无必要过分地加大补偿电容量,一般将功率因数补偿到0.95~0.97之间较为合适。
2 最佳经济点的功率因数
2.1 配电线路损耗减少计算
计算线路损耗时,设有功功率P不变,忽略由于补偿后线电压的升高,则由图1可以得到三相线路损耗减少值为:
△PL=3R×S21×(1-Cos2Φ1/Cos2Φ2/U2(kW) (3)
上式中R为每根配电线电阻(Ω);U为配电线路线电压(kV)。
S1=P/CosΦ1,为补偿前设备视在功率。
上式简化计算可用:
PL =3(I21-I22)
I1及I2分别为补偿前及补偿后电流。2.2 配电变压器损耗减少计算
变损主要由两部分组成,即铜损和铁损。铁损与负荷大小无关,与一次侧外加电压有关,基本恒定不变,铜损与电流平方成比例变化,则配变的损耗减少量为:
△PL=Wte(P/Pe)2×(1-Cos2Φ1/Cos2Φ2)(kW) (4)
其中,Wte为变压器额定铜损;P/ Pe为补偿前配变负荷率。2.3 资金回收期的计算
考虑经济效益,一般用资金回收期计算。设无功就地补偿工程投资为C元,补偿后节约费用L(元/年),则资金回收期Te(年)为:
Te=C/L (5)
式中C=b×Qc
L=(△PT+△PL) ×at
其中,b为每单位千乏的投资费用(元/kvar);
a为电价(元/kwh);
t为设备工作小时数(h)。
所以,Te与功率因数关系式为:
 (6)
(6)
式中A=b×P/at(3RS12/U2+Wte×P2/Pe2)
P=S1×CosΦ1
由(6)可得出
 (7)
(7)
由(2)、(7)式又可得出
Te =A/( 2SinΦ1-Qc/S1) (8)
(2)、(7)、(8)式为功率因数,无功补偿量及经济效益的关系式。
其中,(7)式的关系可表示为CosΦ2=g(Te)的函数形式,是一个单值函数,且当Te =A/SinΦ1时有极大值CosΦ2=1。对于不同的CosΦ1值,以CosΦ2为纵轴,Te /A为横轴,可绘出CosΦ2=g(Te)曲线图如图3所示。
1-CosΦ1=0.5 2-CosΦ1=0.6
3-CosΦ1=0.7 4-CosΦ1=0.8
图3 CosΦ2=g(Te) 曲线图从曲线上看出两大特点:
(1)当CosΦ2小于0.95时,CosΦ2=g(Te)的变化可近似看作直线,但当CosΦ2大于0.95时,随着Te的增大,CosΦ2增长极缓慢。这说明当CosΦ2大于0.95时,资金回收期延长,投资多而功率因数增加不多,经济效益差。
(2)当自然功率因数较高时,要补偿到相同的功率因数,资金回收期大,这说明当自然功率因数高时,尽管所需补偿量小,但从高功率因数补偿到接近1的功率因数是不经济的,效益差。
因此,从经济角度考虑,最佳无功就地补偿功率因数为0.95~0.97,与前面的分析内容吻合。
如上所述,从理论上分析了功率因数,无功补偿量和资金回收期三者的关系,并导出公式。确定出无功就地补偿最佳功率因数是0.95~0.97的范围,在此范围内,既可满足电网的正常动作,亦可以满足经济指标。
 |
 |
 |
 |
 |
 |
- 下载排行更多»
-
- 1Power Panel宣传样本
- 2公司形象手册
- 3工业PC宣传样本
- 4集成自动化宣传样本
- 5驱动器产品概览样本
- 6贝加莱CNC技术
- 7电机与减速器产品概览
- 8变频器样本
- 9移动车辆及工程机械自动化
- 10Automotion 2013-03
- 11印刷行业专刊(2013)
- 12培训模块之 TM213-自动化操作系统(Runti..
- 13培训模块之 TM210-Automation Studio 3.0..
- 14操作面板和工业PC选型手册
- 15电机和减速器选型手册
- 16APROL DCS宣传样本
- 17APROL EnMon宣传样本
- 182013年菲尼克斯电气德国汉诺威展会精彩回顾
- 192013年菲尼克斯电气德国汉诺威展会报道-4..
- 202013年菲尼克斯电气德国汉诺威展会报道-4..
- 212013年菲尼克斯电气德国汉诺威展会报道-4..
- 222013年菲尼克斯电气德国汉诺威展会报道-4..
- 在线反馈
| 1.我有以下需求: | |
|
|
|
| 2.详细的需求: | |
| * | |
| 姓名: | * |
| 单位: | |
| 电话: | * |
| 邮件: | * |





.jpg)



